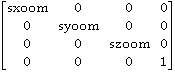
The traditional 9 parameter model performs rigid-body rotations
and translations, followed by independent rescaling along the
resultant x, y, and axes. Many would refer to this as the "Talairach
model", but I have avoided this terminology because 1) Talairach,
et.al, actually used a 13 parameter model that combined 12 such
transformations in a piecemeal fashion, 2) much (or even most) of the
published data alleged to be in "Talairach space" was transformed
into that space using nonlinear transformations, not the traditional
9 parameter transformation described here, 3) unless the target to
which you are registering has been properly oriented with respect to
the AC-PC line, etc., this model will not allow you to report
Talairach coordinates, and 4) this is not the optimum linear model in
the AIR package to use for intersubject registration and I don't want
to implicitly endorse this model as the model to use to derive
Talairach coordinates. My general advice is to use the affine model
to perform linear registration to a Talairach target or else to
procede to a nonlinear technique. I reserve the traditional 9
parameter model for situations where I have reason to believe that
rescaling truly should be applied along a certain set of axes (e.g.,
when I think that the standard file voxel dimensions that I am using
might be incorrect, or when they are unknown).
Since the AIR package allows anisotropic voxels sizes within a given
file as well as different voxel sizes between files, these factors
must be taken into account when applying a traditional 9 parameter
transformation. In the AIR package, the traditional 9 parameter model
is parameterized in terms of rotations around and
translations along each of the three major
coordinate axes and independent rescaling
terms along each of the three major axes of the standard file. In
order to make these parameters more inituitive, the rotations of the
transformation are defined as taking place around the centers of the
files rather than the origin of the
internal coordinate system (located at
one corner of the file).
The traditional 9 parameter transformation for converting from an
internal coordinate in the standard file to the corresponding
internal coordinate in the reslice file is best expressed as the
product of a series of homogenous
transformation matrices:
(reslice file internal coordinates)=Zr*Cr*T*R*G*P*Cs*Zs*(standard
file internal coordinates)
Zs=
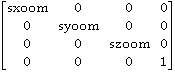
where:
sxoom=(standard file voxel x size) / (smallest standard file voxel size)
syoom=(standard file voxel y size) / (smallest standard file voxel size)
szoom=(standard file voxel z size) / (smallest standard file voxel size)
smallest standard file voxel size=min(standard file voxel x, y and z sizes)
This homogenous transformation matrix remaps coordinate locations in the standard file to new coordinates with cubic voxels. The origin remains at (0,0,0).
Cs=
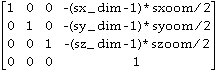
where:
sx_dim=standard file x-dimension
sy_dim=standard file y-dimension
sz_dim=standard file z-dimension
sxoom=(standard file voxel x size) / (smallest standard file voxel size)
syoom=(standard file voxel y size) / (smallest standard file voxel size)
szoom=(standard file voxel z size) / (smallest standard file voxel size)
smallest standard file voxel size=min(standard file voxel x, y and z sizes)
This homogenous coordinate transformation matrix shifts the origin from (0,0,0) to the exact center of the standard file.
P=
![]()
where:
ssize=min(standard file voxel x, y and z sizes)
rsize=min(reslice file voxel x, y and z sizes)
Coordinate units are modified by this homogenous coordinate transformation matrix to be equivalent to those used in an interpolated version of the reslice file.
S=

This homogenous coordinate transformation matrix rescales independently along the major axes of the standard file.
R=

This homogenous coordinate transformation matrix performs rotations while preserving Euclidean distances between coordinate locations.
T=

This homogenous coordinate transformation matrix performs translations while preserving Euclidean distances between coordinate locations.
Note that the shifts have units of interpolated reslice file voxels
Cr=
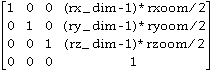
where:
rx_dim=reslice file x-dimension
ry_dim=reslice file y-dimension
rz_dim=reslice file z-dimension
rxoom=(reslice file voxel x size) / (smallest reslice file voxel size)
ryoom=(reslice file voxel y size) / (smallest reslice file voxel size)
rzoom=(reslice file voxel z size) / (smallest reslice file voxel size)
smallest reslice file voxel size=min(reslice file voxel x, y and z sizes)
The origin of the coordinate system is shifted from the center of the file to internal coordinate (0,0,0) of the reslice file by this homogenous coordinate transformation matrix.
Zr=
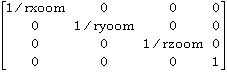
where:
rxoom=(reslice file voxel x size) / (smallest reslice file voxel size)
ryoom=(reslice file voxel y size) / (smallest reslice file voxel size)
rzoom=(reslice file voxel z size) / (smallest reslice file voxel size)
smallest reslice file voxel size=min(reslice file voxel x, y and z sizes)
Cubic voxel coordinate locations are remapped to the actual voxel locations in the reslice file by this homogenous coordinate transformation matrix. The origin (0,0,0) remains unchanged.
Since the standard file interpolation matrix Zs is already implicit in the definition of the.air file transformation matrix, it is omitted from the matrix defined above when creating the .air file matrix: Zr*Cr*T*R*S*P*Cs.
Initialization files for the traditional 9 parameter model consist of the following in ASCII format:
The reslice file voxel units referred to above are cubic (i.e., already interpolated to correct for reslice file voxel size anisotropy).
If no initialization file is specified, the default initialization for programs using a traditional 9 parameter model is:
This results in the exact centers of the two files being aligned to one another.
There are many different ways to define a traditional 9 parameter transformation. Without explicit equations such as those provided above, the terms x_scale,y_scale, z_scale, pitch, roll, yaw, x-shift, y-shift, and z-shift are ambiguous. Other packages for registering or displaying images may not apply the transformations in the same order as the AIR package, so simple substitution of nominal parameters called "pitch","roll", etc. from other packages may not produce the desired result. In moving from standard file coordinates to reslice file coordinates, the AIR package performs x-,y-,and z-scaling, then rotations around the z-axis (yaw), x-axis (pitch), and y-axis (roll) in that order followed by translations x-shift, y-shift, and z-shift. Rotations operate around the exact centers of the files (before and after interpolation) and the sign conventions for both rotations and translations are arbitrary and may differ from those used in your alternative package. Shifts are defined in a version of reslice file space that has been interpolated to cubic voxels and are expressed in units of cubified voxels.
If your alternative package generates a linear algebraic transformation matrix of its own, don't forget that transformation matrices are dependent upon the coordinate system used and that the AIR internal coordinate system used to define transformation matrices may differ from that of your alternative package.
 Modified: December 16, 2001
Modified: December 16, 2001