• 4x1 homogenous coordinate vectors
• 4x4 homogenous coordinate matices
• translations
• rotations
• rescaling
• perspective

Homogenous coordinates utilize a mathematical trick to embed three-dimensional coordinates and transformations into a four-dimensional matrix format. As a result, inversions or combinations of linear transformations are simplified to inversion or multiplication of the corresponding matrices. Homogenous coordinates also make it possible to define perspective transformations.

4x1 Homogenous Coordinate Vectors

Instead of representing each point (x,y,z) in three-dimensional space with a single three-dimensional vector:


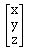
homogenous coordinates allow each point (x,y,z) to be represented by any of an infinite number of four dimensional vectors:


The three-dimensional vector corresponding to any four-dimensional vector can be computed by dividing the first three elements by the fourth, and a four-dimensional vector corresponding to any three-dimensional vector can be created by simply adding a fourth element and setting it equal to one.

Many textbooks define homogenous coordinates in such a way that points are represented by 1x4 vectors:

[T*x T*y T*z T]

instead of 4x1 vectors. This definition is not used in the AIR package and results in different 4x4 homogenous coordinate transformation matrices than those described below.

4x4 Homogenous Coordinate Transformation Matrices

Homogenous coordinate transformation matrices operate on four-dimensional homogenous coordinate vector representations of traditional three-dimensional coordinate locations. Any three-dimensional linear transformation (rotation, translation, skew, perspective distortion) can be represented by a 4x4 homogenous coordinate transformation matrix. In fact, because of the redundant representation of three space in a homogenous coordinate system, an infinite number of different 4x4 homogenous coordinate transformation matrices are available to perform any given linear transformation. This redundancy can be eliminated to provide a unique representation by dividing all elements of a 4x4 homogenous transformation matrix by the last element (which will become equal to one). This means that a 4x4 homogenous transformation matrix can incorporate as many as 15 independent parameters. The generic format representation of a homogenous transformation equation for mapping the three dimensional coordinate (x,y,z) to the three-dimensional coordinate (x',y',z') is:

If any two matrices or vectors of this equation are known, the third matrix (or vector) can be computed and then the redundant T element in the solution can be eliminated by dividing all elements of the matrix by the last element.

Various transformation models can be used to constrain the form of the matrix to tranformations with fewer degrees of freedom.

In many textbooks, you will find homogenous tranformation matrices defined such that 1x4 homogenous coordinate vectors are placed to the left of the 4x4 homogenous coordinate transformation matrix and multiplied. This format is not supported in the AIR package and the difference accounts for the fact that translations are represented in the fourth column and perspective distortions in the fourth row of AIR homologous transformation matrices rather than vice versa.

Translations

Translations can be represented by the 4x4 homogenous coordinate transformation matrix:

Rotations

A series of rotations (in the order [roll matrix]*[pitch matrix]*[yaw matrix]) can be represented by the 4x4 homogenous coordinate transformation matrix:

Rescaling

Rescaling along the major axes can be represented by the 4x4 homogenous coordinate transformation matrix:

Perspective

Perspective distortion is achieved by applying the 4x4 homogenous coordinate transformation matrix: